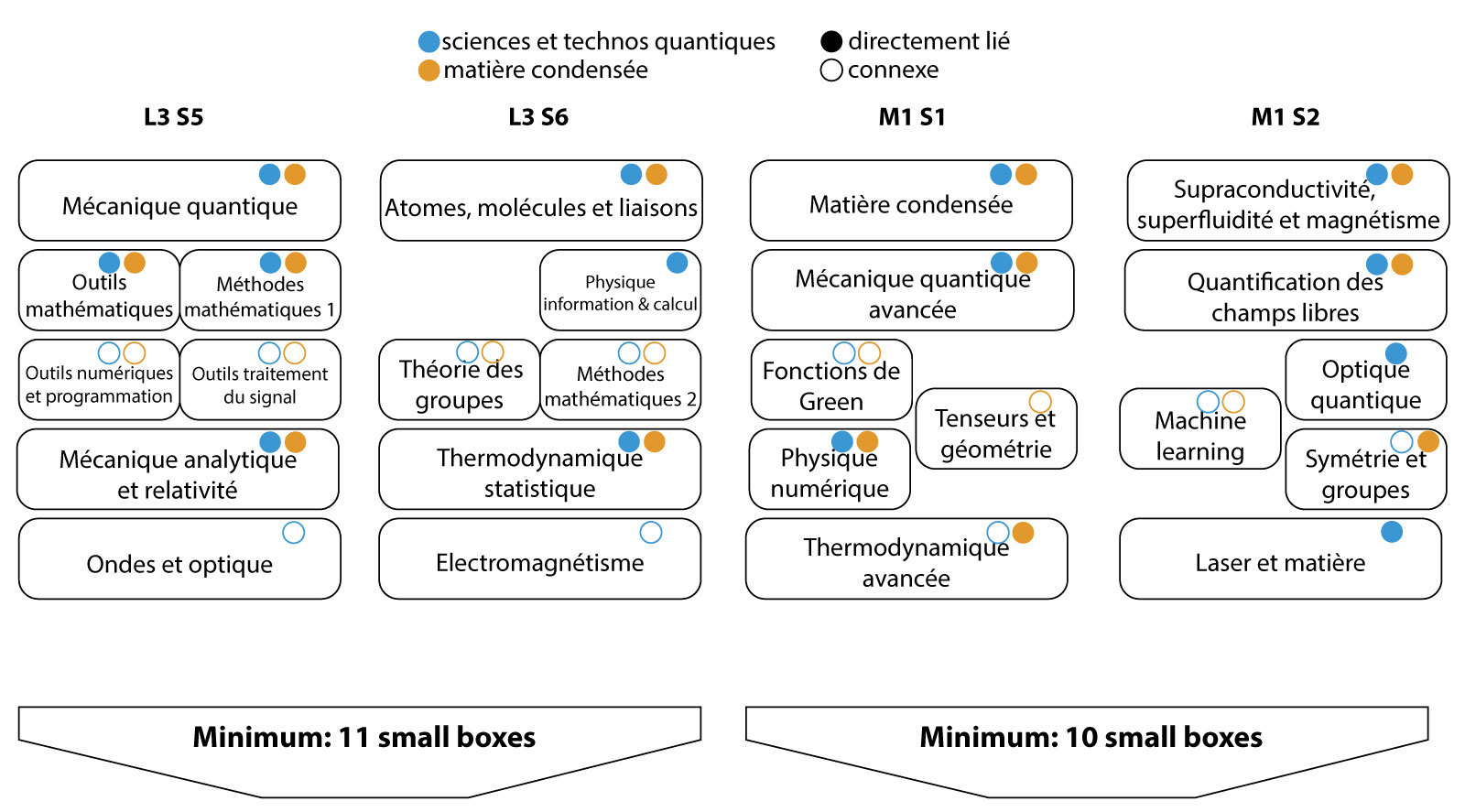
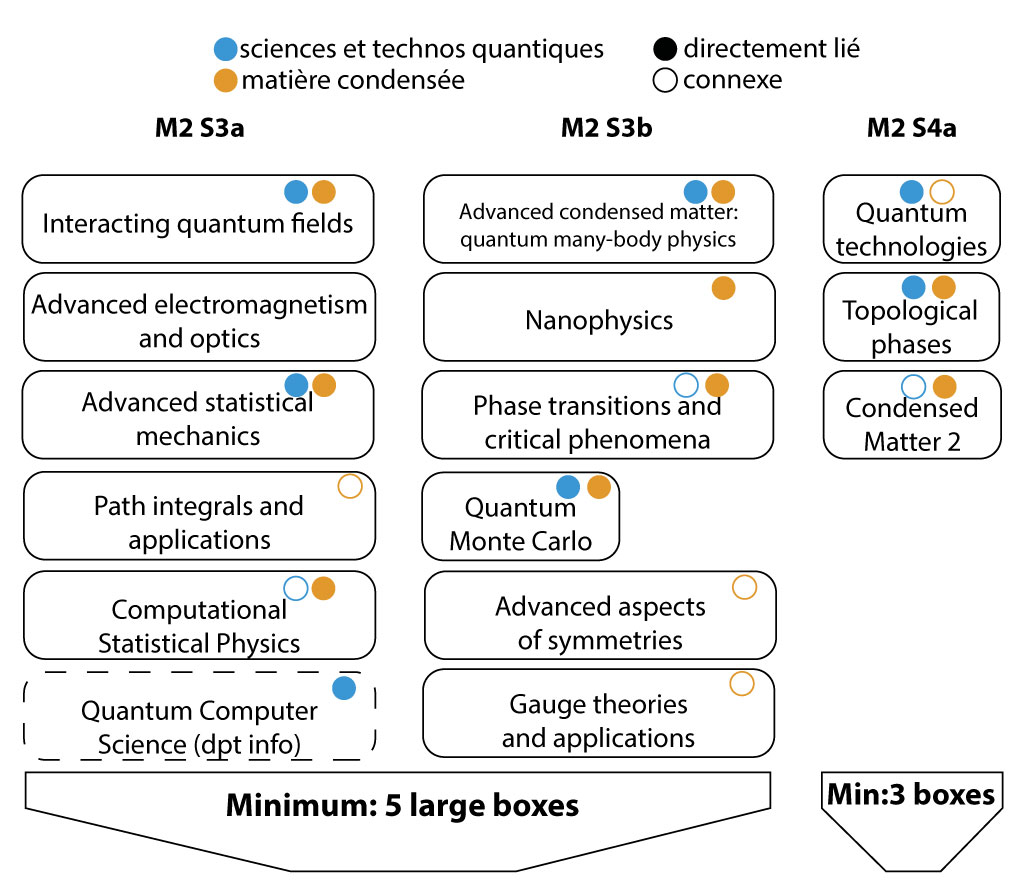
RESEARCH
Quantum Circuit Group

Our research group explores the physics of information in quantum devices, which we design, realize and measure. These objects can be viewed as quantum machines processing information. In contrast with ordinary devices, in which quantum mechanics enters only at the level of individual electrons, the degrees of freedom of these machines at the signal level behave according to the laws of quantum mechanics.
Topics of our current interest include amplification of quantum signals, electron spin resonance at the nanoscale, quantum feedback and trajectory, thermodynamics of quantum information, microwave quantum optics, quantum error correction and quantum measurement. Principal investigators: Audrey Bienfait, Sylvain Hermelin, Benjamin Huard.
ENIQMA (ENtangled Interacting Quantum MAtter) group
Our research group works on the theory of quantum many-body systems; and in particular on how quantum many-body physics can be harnessed to prepare, certify and exploit entangled quantum states of large ensembles of particles. We make use of state-of-the-art theoretical and numerical approaches to study equilibrium states as well as the dynamics of many-body systems far from equilibrium. And we develop scalable methods to certify entanglement as well as other properties of quantum correlation (quantum coherence, Bell nonlocality, etc.). Our predictions are inspired by the works of several experimental groups developing quantum simulations with atomic-physics platforms, or working on quantum correlations in quantum materials. Principal investigators: Fabio Mezzacapo,Tommaso Roscilde.
Electronic quantum optics
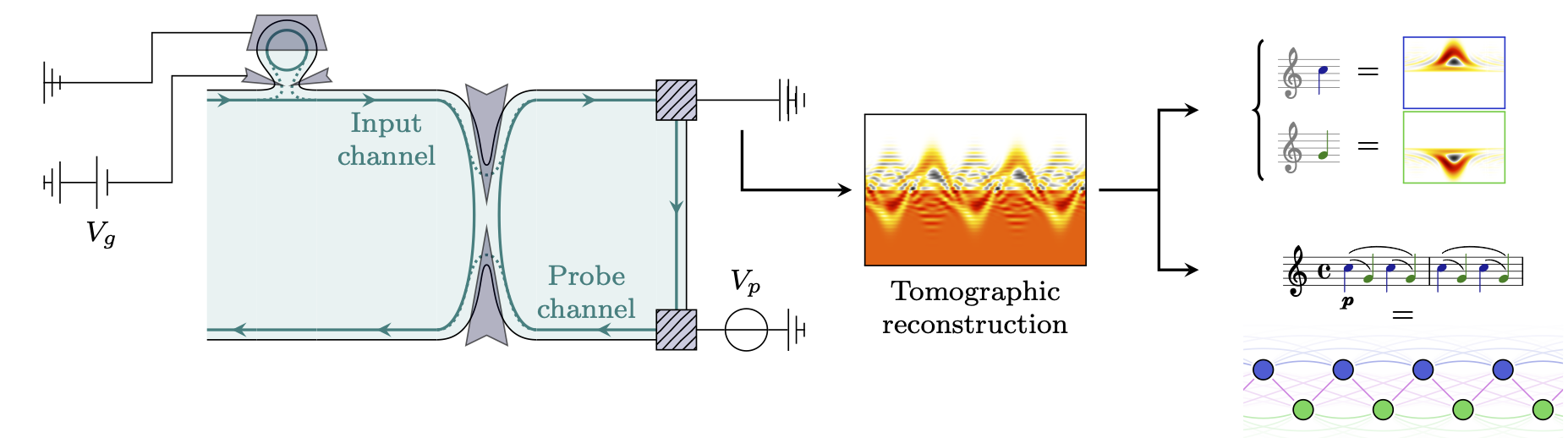
Thanks to technological advances in nanofabrication and radio-frequency techniques, it has become possible to explore the physics of electronic circuits in the regime where quantum effects dominate, and even to prepare, manipulate and measure their quantum states. In particular, it is now possible to generate, characterize and manipulate electrical currents made up of one to a few electrons in well-defined quantum states. This emerging field is known as electronic quantum optics.
Our current research aims to develop a theoretical framework for electron quantum optics, an emerging field that aims to manipulate the quantum state of one or a few electrons in a conductor. This ultimate form of electric current is now sufficiently well controlled for applications to be envisaged. We are interested in the measurement of microwave electromagnetic fields with pico-second time resolution using single-electron interferometers, in the use of single electron wave packets as quantum information carriers (electron qubits), and in the study of quantum electromagnetic radiation radiated by such quantum electric currents. Finally, we are interested in studying and characterizing the quantum entanglement conveyed by these currents. Principal investigator: Pascal Degiovanni.
QInfo team

QInfo is an Inria Project-Team focusing on quantum information. We develop mathematical and algorithmic tools to make optimal use of quantum information resources. Information-processing devices that can take advantages of the laws of quantum theory have an important potential in terms of computation, communication and secrecy. However, the quantum devices available today are all affected by unwanted noise: the actual behavior of the device only matches approximately with the model they were designed for. Such an unwanted deviation from the model can have devastating effects for the information processing applications: for example, in the context of quantum computation, the accumulation of noise can render the outcome of the computation completely useless. This project aims to develop methods and algorithms to optimally reduce the undesirable effect caused by noise on quantum information processing tasks. Principal investigators: Alastair Abbott, Guillaume Aubrun, Omar Fawzi, Daniel Stilck França, Mischa Woods.
Theory of Quantum Matter
Our research group works on various theoretical research directions in the field of quantum matter, with the goal of elucidating the physical properties of new quantum phases of matter, particularly magnetic properties, electrical and thermal transport. They employ and develop a diverse array of theoretical tools, including numerical techniques such as variational Monte Carlo methods, finite-temperature quantum Monte Carlo, exact diagonalization, as well as analytical methods such as bosonization, diagrammatic methods in field theory, renormalization group, and variational methods. This allows them to tackle a wide range of situations where correlations, quantum fluctuations, or long-range interactions play important roles. Among other topics, the team investigates spin ice and its magnetic excitations, non-equilibrium dynamics and droplet formation in cold atom gases, spin liquids, as well as the effects of disorder-induced localization in Dirac and Weyl semimetals, in connection with the theme of Topological Systems.Principal investigators: Peter Holdsworth, Edmond Orignac, Lucile Savary.
Theory of topological systems
Our team combines various numerical and analytical techniques (adiabatic theory, semiclassical methods, field theory) and draws from mathematics (differential geometry, index theorems) to describe the topological aspects of a wide range of physical systems. We are particularly interested in study the interplay between topological properties and other aspects, such as disorder, nonlinearity, or non-Hermiticity in these systems. In the quantum domain, for example, we are interested in Weyl semimetals, artificial gauge fields with cold atoms, quantum dynamics induced by topological couplings between different degrees of freedom, and the emergence of analog gravitational effects in certain topological materials. In the classical domain, we explore new topological states in mechanics, photonics, acoustics, as well as in fluids, with applications in geophysics and astrophysics involving wave phenomena.Principal investigators: David Carpentier, Pierre Delplace, Andrei Fedorenko.
Math
The Unité de Mathématiques Pures et Appliquées (UMPA), ENSL's mathematics laboratory, is active in mathematical physics, particularly in its "Analysis and Modeling" and "Probability" teams. Themes at the interface with quantum physics are well represented: N-body quantum mechanics, mean-field limits (Laurent Laflèche, Nicolas Rougerie), Analyse semi-classique (Paul Alphonse, Laurent Laflèche), semi-classical analysis (Paul Alphonse, Laurent Laflèche), dispersive partial differential equations (Nicolas Rougerie, Nikolay Tzvetkov), Random matrices and tensors (Alice Guionnet), Stochastic quantization, Euclidean quantum field theory (Jean-Christophe Mourrat, Nicolas Rougerie), Spin glasses (Jean-Christophe Mourrat), Operator algebras (Amine Marrakchi)